【人気ダウンロード!】 the identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 167187
If X Y 2 Then What Is The Value Of X Y 6xy Quora
F(x,y) = x3 − 3xy2 is an example satisfying the Laplace equation 7 The advection equation ft = fx is used to model transport in a wire The function f(t,x) = e−(xt)2 satisfy the advection equation 8 The eiconal equation f2 x f2 y = 1 is used to see the evolution of wave fronts in optics The function f(x,y) = cos(x) sin(y) satisfiesClick here👆to get an answer to your question ️ Verify x^3 y^3 = (x y)(x^2 xy y^2) using some non zero positive integers and check by actual multiplication Can you call theses as identities?
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2-1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials informationPartial Differential Equations Exam 1 Review Solutions Spring 18 Exercise 1 Verify that both u= log(x2y2) and u= arctan(y=x) are solutions of Laplace's equation u xx u yy= 0 If u= log(x2 y2), then by the chain rule u x= 2x x 2 y) u xx= (x2 y2)(2) (2x)(2x) (x 2 y) 2y2 2x2 (x y2)2 and by the symmetry of uin xand y,

October 17 Mr Honner
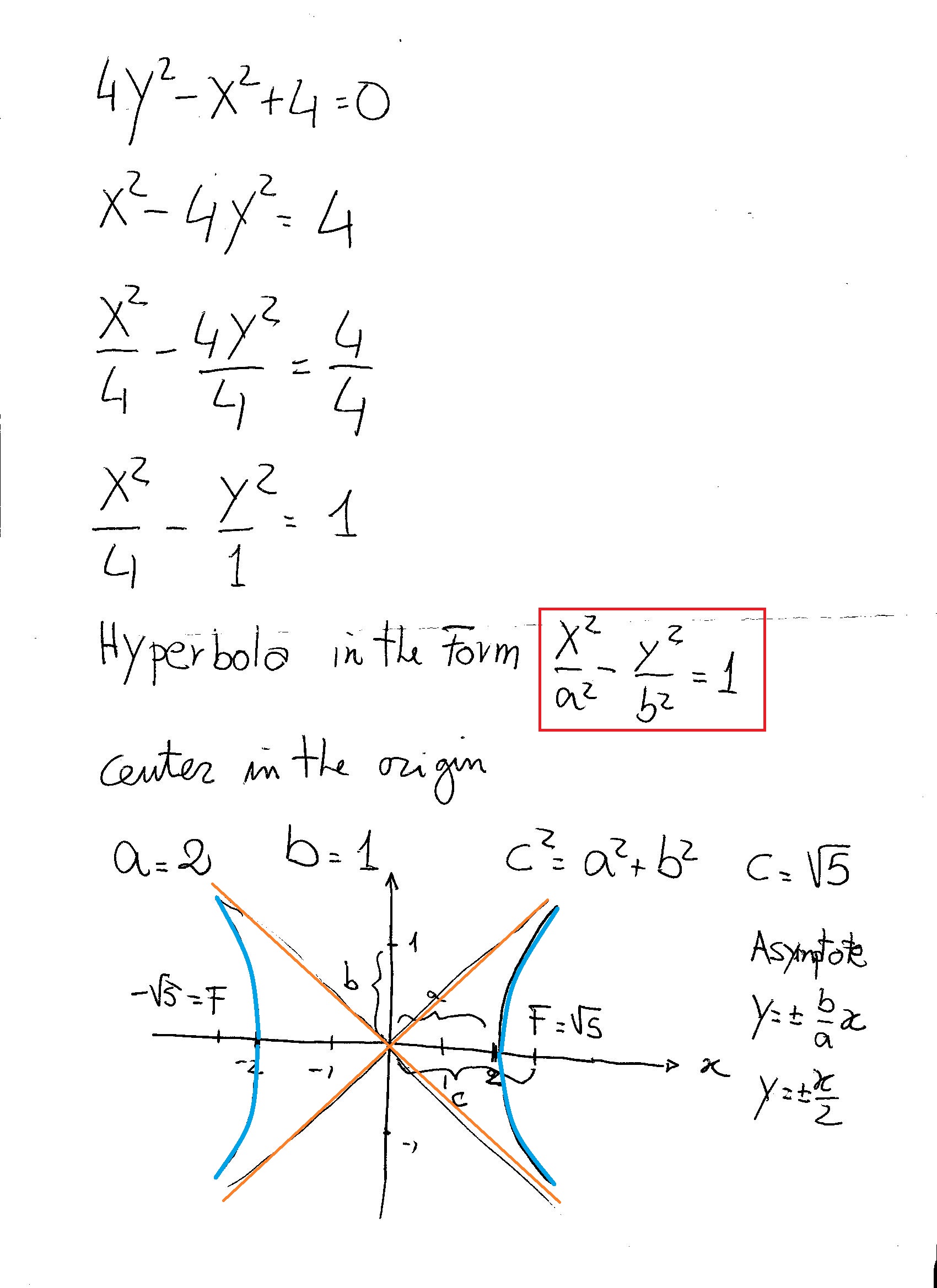
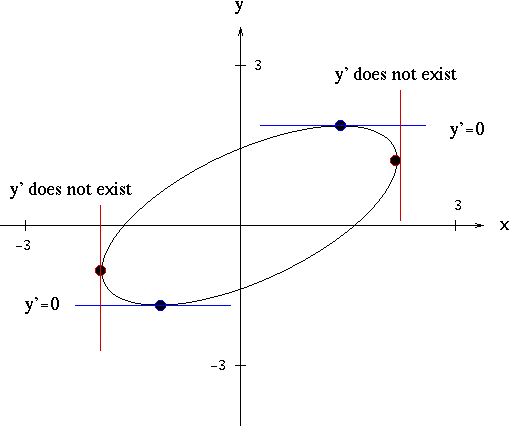
All those who say programming isn't for kids, just haven't met the right mentors yet Join the Demo Class for First Step to Coding Course, specifically designed for students of class 8 to 12 The students will get to learn more about the world of programming in these free classes which will definitely help them in making a wise career choice in the future Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeTrigonometry Graph x^2y^22x2y1=0 x2 − y2 − 2x − 2y − 1 = 0 x 2 y 2 2 x 2 y 1 = 0 Find the standard form of the hyperbola Tap for more steps Add 1 1 to both sides of the equation x 2 − y 2 − 2 x − 2 y = 1 x 2 y 2 2 x 2 y = 1 Complete the square for x 2 − 2 x x 2 2 x
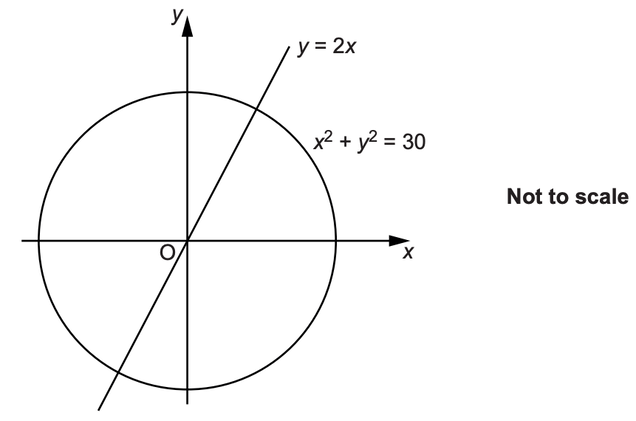
And x>y This is what I got x^2y^2xy=2 x^2*2ydy/dx 2x*y^2 x*dy/dx y =0 dy/dx(2yx^2x)= 2xy^2y dy/dx = (2xy^2y)/(x2yx^2) how do ILHS = x3 y3 z3 3xyz= (x y x) (x2 y2 z2 xy yz zx) Using Identity VIII (xyz){2x2 2y2 z2 xy yz zx) (xyz){2x2 2y2 2z2 2xy 2yz 2zxAnswer Given 2x2 y2 8z2 – 2√2xy 4√2yz – 8xz Using identity, (x y z)2 = x2 y2 z2 2xy 2yz 2zx We can say that, x 2 y 2 z 2 2xy 2yz 2zx = (x y z) 2 2x 2 y 2 8z 2 – 2√2xy 4√2yz – 8xz = (√2x) 2 (y) 2 (2√2z) 2 (2 × √2x × y) (2 × y × 2√2z) (2 × 2√2 × √2x) = (√2x y 2√2z) 2
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 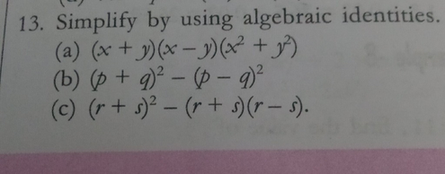 | |
 |  |  |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 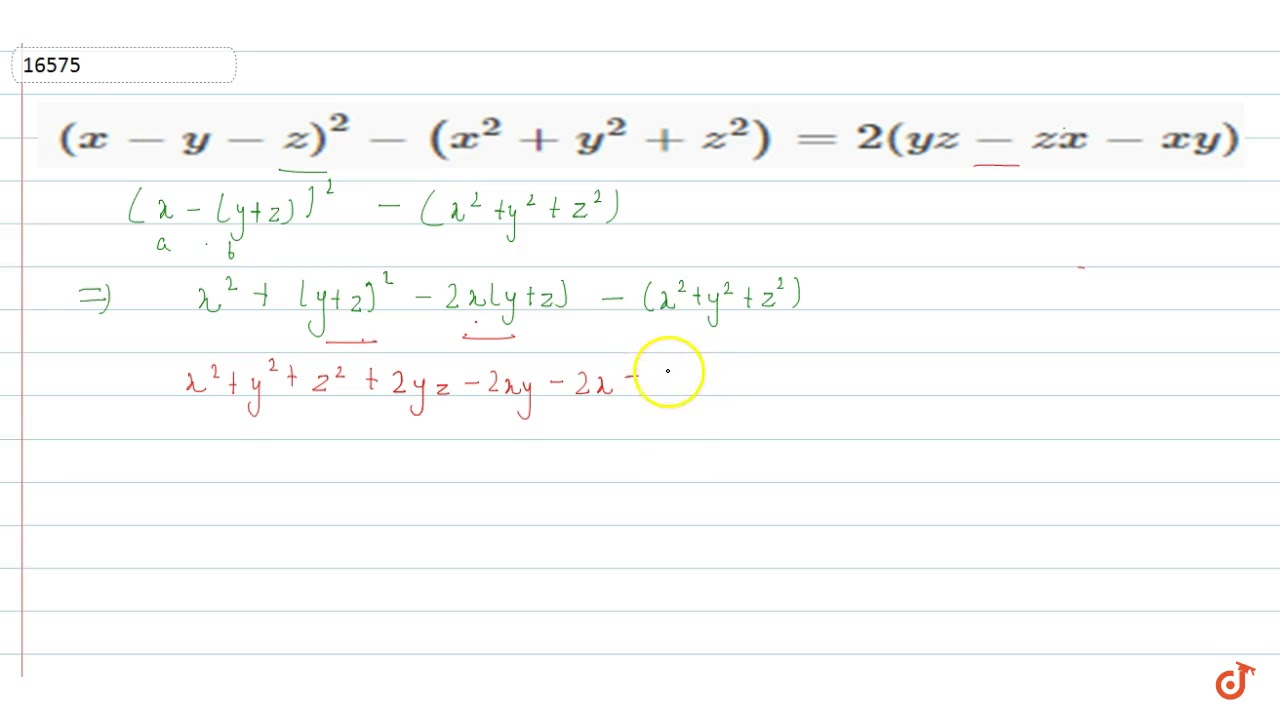 |
 | ||
 | ||
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 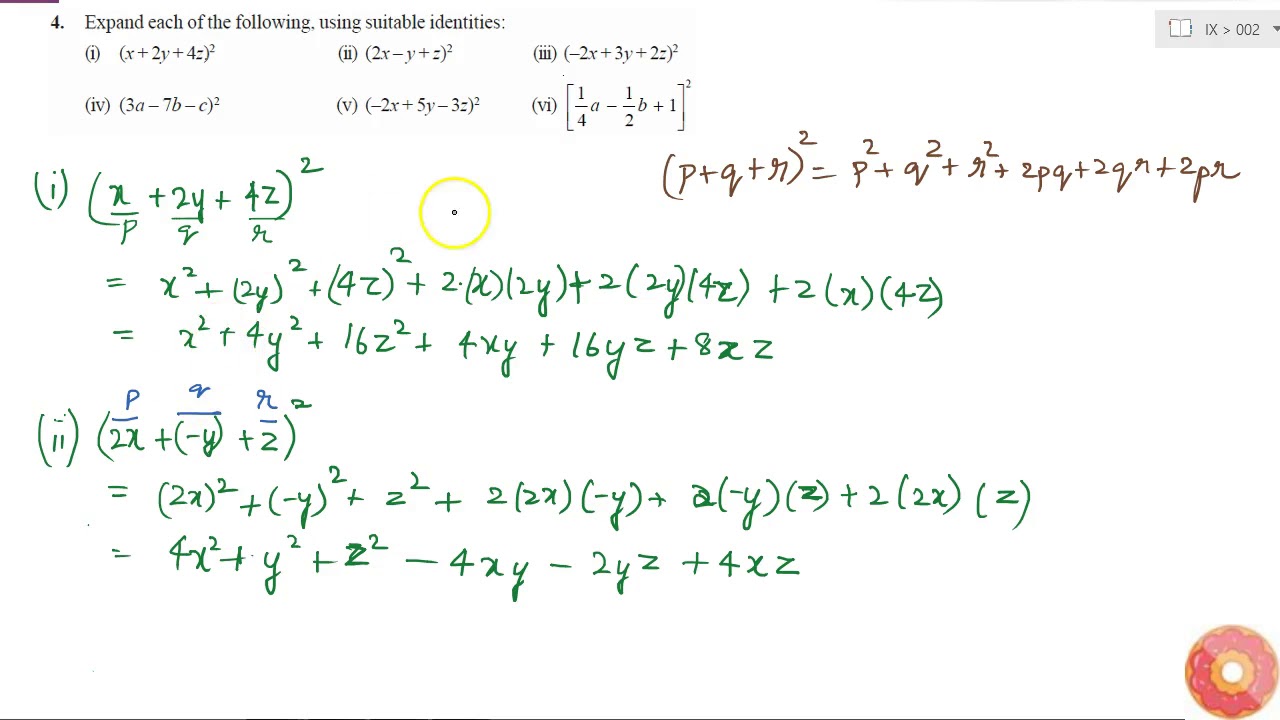 | |
 | ||
 |  |  |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | 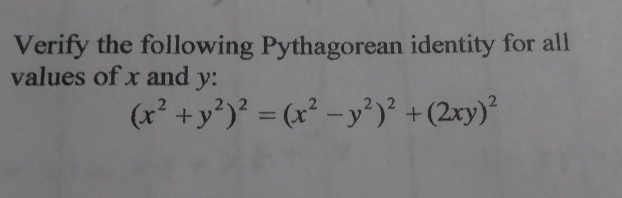 | |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 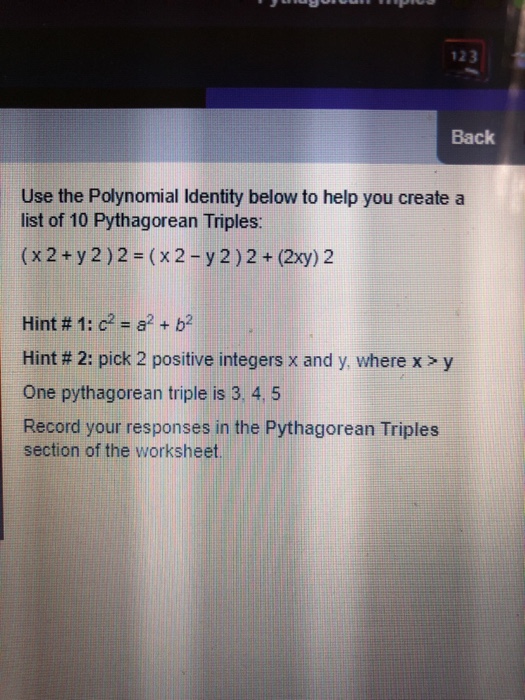 |
 |  | |
「The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the square of a binomial, etcHowever, there will be several terms of the form x n−2 y 2, one for each way of choosing exactly two binomials to contribute a y Therefore, after combining like terms, the coefficient of x n−2 y 2 will be equal to the number of ways to choose exactly 2 elements from an nelement set Proofs Combinatorial proof Example
コメント
コメントを投稿